In the last post we had a simple stepping algorithm, and a gradient descent implementation, for fitting a line to a set of points with one variable and one ‘outcome’. As I mentioned though, it’s fairly straightforward to extend that to multiple variables, and even to curves, rather than just straight lines.
For this example I’ve reorganised the code slightly into a class to make life a little easier, but the main changes are just the hypothesis and learn functions. For the hypothesis, we just need to calculate our output value based on all of the parameters, so we turn our calculation into a loop:
<?php
/**
* Generate a score based on the data and passed parameters
*
* @param array $params
* @return int
*/
protected function mv_hypothesis($rowdata, $params) {
$score = $params[0];
foreach($rowdata as $id => $value) {
$score += $value * $params[$id+1];
}
return $score;
}
?>Similarly, we need to update our learning function. In the single parameter case we were using updating our intercept based on the score, and then we were multiplying our gradient (the second parameter) by the example row’s value - so our gradient would be multiplied by the example’s x score. We’re going to do the same here, updating each parameter after the first with the value multiploed by the example’s xn value - so parameter1 * x0, parameter2 * x1 and so on.
<?php
/**
* Update the parameters, including using a dummy row value
* of 1 for the first parameter.
*
* @param array $params
* @return array
*/
protected function learn($params) {
$data_rate = 1/count($this->data);
foreach($params as $id => $p) {
foreach($this->data as $row) {
$score = $this->mv_hypothesis($row[0], $params) - $row[1];
// Update parameters
$params[$id] -= $this->learning_rate *
($data_rate *
( $score * ($id == 0 ? 1 : $row[0][$id-1]) )
);
}
}
return $params;
}
?>The rest stays pretty much the same - each step we update the parameters in the learn function, and check that our score is reducing properly. However, one of the other issues we didn’t look very much in the previous post was what learning rate to choose, and what number of iterations to limit to. These are often hard to say precisely, but it can help to plot the change in the score for different values on a graph. We can do that for some data with our class pretty easily.
<?php
/* Nice regular data for testing */
$data = array(
array(array(2, 4000, 0.5), 2+2+(2*4)+(3*5)),
array(array(2, 4000, 0.4), 2+2+(2*4)+(3*4)),
array(array(2, 4000, 0.6), 2+2+(2*4)+(3*6)),
array(array(1, 5000, 0.5), 2+1+(2*5)+(3*5)),
array(array(2, 5000, 0.1), 2+2+(2*5)+(3*1)),
);
$iterations = array(10, 100, 500, 1000, 2000, 5000, 10000);
$mvg = new MVGradient();
$mvg->set_data($data);
foreach(array(0.1, 0.01, 0.001, 0.001) as $rate) {
$mvg->set_learning_rate($rate);
foreach($iterations as $i) {
$params = $mvg->find_params($i);
echo $mvg->score($params), "\n";
}
echo "\n";
}
?>Plotting the output gives us a graph like this:
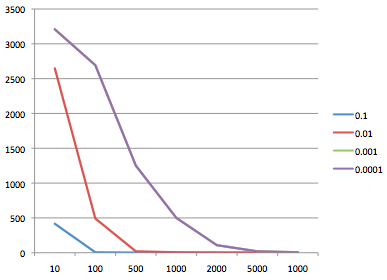
We can see from the graph that the error rate is reducing well with 0.1, so that would be a good start point for this data. However, if the learning rate is too high, the graph may bounce around, or not converge as well, which would be a sign to reduce it.
One other new thing we’re doing in this code is trying to standardise the data a bit by scaling it between -0.5 and 0.5. To do that, we calculate the min and max of any given feature (so e.g. the min and max of values x1 say) to give us the range of values. We also calculate the average for each entry.
For each value we then subtract the average (giving it a nice mean of 0), and divide by the different between min and max, which gives us the -0.5 to 0.5 range. This allows us to treat data at different scales similarly, which tends to be a win for the algorithm (though not always, so your mileage may vary) - as in real world problems we’ll often be dealing with data that has entries at very diverse ranges - for example if we’re trying to estimate the value of companies based on the number of employees and number of office locations, we’re could well be talking about numbers in the 1000s for employees by 10s for office. Gradient descent will still work without feature scaling, but it’ll take longer.
<?php
/**
* Normalise variance and scale data to:
* xi - avg(xi) / range(max-min)
* so we get in a -0.5 - 0.5 range with an
* avg of 0
* - this is a bit of clunky method!
*/
protected function scale_data($data) {
$minmax = array();
$rows = count($data);
foreach($data as $key => $row) {
foreach($row[0] as $id => $val) {
/* Initialise Arrays */
if(!isset($minmax[$id])) {
$minmax[$id] = array();
$minmax[$id]['min'] = false;
$minmax[$id]['max'] = false;
$minmax[$id]['total'] = 0;
}
/* Get stats */
if( $minmax[$id]['min'] == false ||
$minmax[$id]['min'] > $val) {
$minmax[$id]['min'] = $val;
}
if( $minmax[$id]['max'] == false ||
$minmax[$id]['max'] < $val) {
$minmax[$id]['max'] = $val;
}
$minmax[$id]['total'] += $val;
}
}
/* Compute average and variance */
foreach($minmax as $id => $row) {
$minmax[$id]['var'] = $row['max'] - $row['min'];
$minmax[$id]['avg'] = $row['total'] / $rows;
}
foreach($data as $key => $row) {
foreach($row[0] as $id => $val) {
$data[$key][0][$id] = ( $val - $minmax[$id]['avg'] )
/ $minmax[$id]['var'];
}
}
return $data;
}
?>One other interesting thing we can do once we have this kind of setup is to extend it to lines (or surfaces in the > 2D cases) that are not straight - using polynomials (anything with an x2 or higher power) in it. All we have to do for that is update our hypothesis and learn functions again so that we calculate the hypothesis with the right powers on the variables, and update our learn function.
If you recall from the previous article, the learning function was updating based on the partial derivative of our ‘cost’ function (the sum of the squared errors between prediction and actual values) - we’re doing the same here. For the linear case we had to multiply the score by the value of xn, so parameter1’s was updated by the score multiplied by x0 and so on. In this case, we need to make sure we include the power, so if our hypothesis is is y = parameter0 + parameter1*x02 then we need to multiply parameter1 by x02 in the learning function.
<?php
class PolyMV extends MVGradient {
/**
* Skip scaling just for the example
*/
protected function scale_data($data) {
return $data;
}
/**
* Generate a score based on the data and passed parameters
*
* @param array $params
* @return int
*/
protected function mv_hypothesis($rowdata, $params) {
$score = $params[0];
foreach($rowdata as $id => $value) {
$score += pow($value, $id+2) * $params[$id+1];
}
return $score;
}
/**
* Update the parameters, including using a dummy row value
* of 1 for the first parameter.
*
* @param array $params
* @return array
*/
protected function learn($params) {
$data_rate = 1/count($this->data);
foreach($params as $id => $p) {
foreach($this->data as $row) {
$score = $this->mv_hypothesis($row[0], $params) - $row[1];
// Update parameters
// We have to multiply by an appropriate power as part of the
// partial derivative
$params[$id] -= $this->learning_rate *
($data_rate *
( $score *
($id == 0 ? 1 : pow($row[0][$id-1], $id+1)) )
);
}
}
return $params;
}
}
?>We can then call that function exactly the same way. As the ml-class lectures point out, there is a quicker way of getting this for many cases (ones with reasonable numbers of features, or xn values), which is called the normal method - but that involves some linear algebra in calculating the inverse of a matrix - something that there isn’t a library for in PHP (as far as I’m aware), and hence a bit of a pain to write -but if you are interested in solving these types of problems, it’s worth looking into.
